Kernel Case Examine: Flash Consideration

mechanism is on the core of contemporary day transformers. However scaling the context window of those transformers was a serious problem, and it nonetheless is despite the fact that we’re within the period of 1,000,000 tokens + context window (Qwen 2.5 [1]). There are each appreciable compute and reminiscence certain complexities in these fashions after we scale the context window (A naive Consideration Mechanism scales quadratically in each compute and reminiscence necessities). Revisiting Flash Consideration lets us perceive the complexities of optimizing the underlying operations on GPUs and extra importantly offers us a greater grip on pondering what’s subsequent.

Let’s shortly revisit a naive consideration algorithm to see what’s occurring.

As you’ll be able to see if we’re not being cautious then we are going to find yourself materializing a full NxM consideration matrix into the GPU HBM. Which means the reminiscence requirement will go up quadratically to rising context size.

When you wanna be taught extra in regards to the GPU reminiscence hierarchy and its variations, my earlier put up on Triton is an efficient place to begin. This may even be useful as we go alongside on this put up after we get to implementing the Flash Consideration kernel in triton. The flash consideration paper additionally has some actually good introduction to this.

Moreover, after we have a look at the steps concerned in executing this algorithm and its sample of accessing the sluggish HBM, (which as defined later within the put up may very well be a serious bottleneck as properly) we discover a couple of issues:

1. We now have Q, Okay and V within the HBM initially
2. We have to entry Q and Okay initially from the HBM to compute the dot product
3. We write the output scores again to the HBM
4. We entry it once more to execute the softmax, and optionally for Causal consideration, like within the case of LLMs, we must masks this output earlier than the softmax. The ensuing full consideration matrix is written once more into the HBM
5. We entry the HBM once more to execute the ultimate dot product, to get each the eye weights and the Worth matrix to jot down the output again to the sluggish GPU reminiscence

I feel you get the purpose. We might neatly learn and write from the HBM to keep away from redundant operations, to make some potential positive aspects. That is precisely the first motivation for the unique Flash Consideration algorithm.

Flash Consideration initially got here out in 2022 [2], after which a 12 months later got here out with some a lot wanted enhancements in 2023 as Flash Consideration v2 [3] and once more in 2024 with extra enhancements for Nvidia Hopper and Blackwell GPUs [4] as Flash Consideration v3 [5]. The unique consideration paper recognized that the eye operation continues to be restricted by reminiscence bandwidth quite than compute. (Previously, there have been makes an attempt to scale back the computation complexity of Consideration from O(N**2) to O(NlogN) and decrease by means of approximate algorithms)

Flash consideration proposed a fused kernel which does all the above consideration operations in a single go, block-wise, to get the ultimate consideration output with out ever having to understand the complete N**2 consideration matrix in reminiscence, making the algorithm considerably sooner. The time period `fused` merely means we mix a number of operations within the GPU SRAM earlier than invoking the a lot slower journey throughout the slower GPU reminiscence, making the algorithm performant. All of the whereas offering the precise consideration output with none approximations.

This lecture, from Stanford CS139, demonstrates brilliantly how we will consider the influence of a properly thought out reminiscence entry sample can have on an algorithm. I extremely suggest you test this one out in case you haven’t already.

Earlier than we begin diving into flash consideration to name it FA, we could?) in triton there’s something else that I wished to get out of the best way.

Numerical Stability in exponents

Let’s take the instance of FP32 numbers. float32 (customary 32-bit float) makes use of 1 signal bit, 8 exponent bits, and 23 mantissa bits [6]. The most important finite base for the exponent in float32 is 2¹²⁷≈1.7×10³⁸. Which means after we have a look at exponents, e⁸⁸ ≈ 1.65×10³⁸, something near 88 (though in actuality could be a lot decrease to maintain it protected) and we’re in hassle as we might simply overflow. Right here’s a very attention-grabbing chat with OpenAI o1 shared by people at AllenAI of their OpenInstruct repo. This though is speaking about stabilizing KL Divergence calculations within the setting of RLHF/RL, the concepts translate precisely to exponents as properly. So to cope with the softmax state of affairs in consideration what we do is the next:

TRICK : Let’s additionally observe the next, in case you do that:

then you’ll be able to rescale/readjust values with out affecting the ultimate softmax worth. That is actually helpful when you might have an preliminary estimate for the utmost worth, however which may change after we encounter a brand new set of values. I do know I do know, stick with me and let me clarify.

Setting the scene

Let’s take a small detour into matrix multiplication.

This exhibits a toy instance of a blocked matrix multiplication besides we’ve blocks solely on the rows of A (inexperienced) and columns of B (Orange? Beige?). As you’ll be able to see above the output O1, O2, O3 and O4 are full (these positions want no extra calculations). We simply must fill within the remaining columns within the preliminary rows through the use of the remaining columns of B. Like under:

So we will fill these locations within the output with a block of columns from B and a block of rows from A at a time.

Connecting the dots

After I launched FA, I stated that we by no means should compute the complete consideration matrix and retailer the entire thing. So right here’s what we do:

1. Compute a block of the eye matrix utilizing a block of rows from Q and a block of columns from Okay. When you get the partial consideration matrix compute a couple of statistics and preserve it within the reminiscence.

I’ve greyed O5 to O12 as a result of we don’t know these values but, as they should come from the following blocks. We then rework Sb like under:

Now you might have setup for a partial softmax

However:

1. What if the true most is within the Oi’s which might be but to return?
2. The sum continues to be native, so we have to replace this each time we see new Pi’s. We all know easy methods to preserve monitor of a sum, however what about rebasing it to the true most?

Recall the trick above. All that we’ve to do is to maintain a monitor of the utmost values we encounter for every row, and iteratively replace as you see new maximums from the remaining blocks of columns from Okay for a similar set of rows from Q.

We nonetheless don’t need to write our partial softmax matrix into HBM. We preserve it for the subsequent step.

The ultimate dot product

The final step in our consideration computation is our dot product with V. To begin we’d have initialized a matrix filled with 0’s in our HBM as our output of form NxD. The place N is the variety of Queries as above. We use the identical block dimension for V as we had for Okay besides we will apply it row sensible like under (The subscripts simply denote that that is solely a block and never the complete matrix)

Discover how we’d like the eye scores from all of the blocks to get the ultimate product. But when we calculate the native rating and `accumulate` it like how we did to get the precise Ls we will kind the complete output on the finish of processing all of the blocks of columns (Okay_b) for a given row block (Q_b).

Placing all of it collectively

Let’s put all these concepts collectively to kind the ultimate algorithm

To know the notation, __ij implies that it’s the native values for a given block of columns and rows and _i implies it’s for the worldwide output rows and Question blocks. The one half we haven’t defined thus far is the ultimate replace to O_i. That’s the place we use all of the concepts from above to get the precise scaling.

The entire code is out there as a gist right here.

Let’s see what these initializations seem like in torch:

def flash_attn_v1(Q, Okay, V, Br, Bc):
  """Flash Consideration V1"""
  B, N, D = Q.form
  M = Okay.form[1]
  Nr = int(np.ceil(N/Br))
  Nc = int(np.ceil(N/Bc))
  
  Q = Q.to('cuda')
  Okay = Okay.to('cuda')
  V = V.to('cuda')
  
  batch_stride = Q.stride(0)
  
  O = torch.zeros_like(Q).to('cuda')
  lis = torch.zeros((B, Nr, int(Br)), dtype=torch.float32).to('cuda')
  mis = torch.ones((B, Nr, int(Br)), dtype=torch.float32).to('cuda')*-torch.inf
  
  grid = (B, )
  flash_attn_v1_kernel[grid](
      Q, Okay, V,
      N, M, D,
      Br, Bc,
      Nr, Nc,
      batch_stride,
      Q.stride(1),
      Okay.stride(1),
      V.stride(1),
      lis, mis,
      O,
      O.stride(1),
  )
  return O

In case you are uncertain in regards to the launch grid, checkout my introduction to Triton

Take a more in-depth have a look at how we initialized our Ls and Ms. We’re maintaining one for every row block of Output/Question, every of dimension B_r. There are N_r such blocks in whole.

Within the instance above I used to be merely utilizing B_r = 2 and B_c = 2. However within the above code the initialization relies on the system capability. I’ve included the calculation for a T4 GPU. For some other GPU, we have to get the SRAM capability and alter these numbers accordingly. Now for the precise kernel implementation:

# Flash Consideration V1
import triton
import triton.language as tl
import torch
import numpy as np
import pdb

@triton.jit
def flash_attn_v1_kernel(
    Q, Okay, V,
    N: tl.constexpr, M: tl.constexpr, D: tl.constexpr,
    Br: tl.constexpr,
    Bc: tl.constexpr,
    Nr: tl.constexpr,
    Nc: tl.constexpr,
    batch_stride: tl.constexpr,
    q_rstride: tl.constexpr,
    k_rstride: tl.constexpr, 
    v_rstride: tl.constexpr,
    lis, mis,
    O,
    o_rstride: tl.constexpr):
    
    """Flash Consideration V1 kernel"""
    
    pid = tl.program_id(0)
    

    for j in vary(Nc):
        k_offset = ((tl.arange(0, Bc) + j*Bc) * k_rstride)[:, None] + (tl.arange(0, D))[None, :] + pid * M * D
        # Utilizing k_rstride and v_rstride as we're trying on the complete row directly, for every okay v block 
        v_offset = ((tl.arange(0, Bc) + j*Bc) * v_rstride)[:, None] + (tl.arange(0, D))[None, :] + pid * M * D
        k_mask = k_offset < (pid + 1) * M*D
        v_mask = v_offset < (pid + 1) * M*D
        k_load = tl.load(Okay + k_offset, masks=k_mask, different=0)
        v_load = tl.load(V + v_offset, masks=v_mask, different=0)
        for i in vary(Nr):
            q_offset = ((tl.arange(0, Br) + i*Br) * q_rstride)[:, None] + (tl.arange(0, D))[None, :] + pid * N * D
            q_mask = q_offset < (pid + 1) * N*D
            q_load = tl.load(Q + q_offset, masks=q_mask, different=0)
            # Compute consideration
            s_ij = tl.dot(q_load, tl.trans(k_load))
            m_ij = tl.max(s_ij, axis=1, keep_dims=True)
            p_ij = tl.exp(s_ij - m_ij)
            l_ij = tl.sum(p_ij, axis=1, keep_dims=True)
            
            ml_offset = tl.arange(0, Br) + Br * i + pid * Nr * Br
            m = tl.load(mis + ml_offset)[:, None]
            l = tl.load(lis + ml_offset)[:, None]

            m_new = tl.the place(m < m_ij, m_ij, m)

            l_new = tl.exp(m - m_new) * l + tl.exp(m_ij - m_new) * l_ij

            o_ij = tl.dot(p_ij, v_load)

            output_offset = ((tl.arange(0, Br) + i*Br) * o_rstride)[:, None] + (tl.arange(0, D))[None, :] + pid * N * D
            output_mask = output_offset < (pid + 1) * N*D
            o_current = tl.load(O + output_offset, masks=output_mask)

            o_new = (1/l_new) * (l * tl.exp(m - m_new) * o_current + tl.exp(m_ij - m_new) * o_ij)

            tl.retailer(O + output_offset, o_new, masks=output_mask)
            tl.retailer(mis + ml_offset, tl.reshape(m_new, (Br,)))
            tl.retailer(lis + ml_offset, tl.reshape(l_new, (Br,)))

Let’s perceive whats occurring right here:

1. Create 1 kernel for every NxD matrix within the batch. In actuality we’d have yet another dimension to parallelize throughout, the pinnacle dimension. However for understanding the implementation I feel this might suffice.
2. In every kernel we do the next:
   1. For every block of columns in Okay and V we load up the related a part of the matrix (B_c x D) into the GPU SRAM (Present whole SRAM utilization = 2B_cD). This stays within the SRAM until we’re achieved with all of the row blocks
   2. For every row block of Q, we load the block onto SRAM as properly (Present whole SRAM Utilization = 2B_cD + BrD)
   3. On chip we compute the dot product (s_ij), compute the native row-maxes (m_ij), the exp (p_ij), and the expsum (l_ij)
   4. We load up the operating stats for the i^th row block. Two vectors of dimension B_r x 1, which denotes the present international row-maxes (m_i) and the expsum (l_i). (Present SRAM utilization: 2B_cD + B_rD + 2B_r)
   5. We get the brand new estimates for the worldwide m_i and l_i.
   6. We load the a part of the output for this block of Q and replace it utilizing the brand new operating stats and the exponent trick, we then write this again into the HBM. (Present SRAM utilization: 2B_cD + 2B_rD + 2B_r)
   7. We write the up to date operating stats additionally into the HBM.
3. For a matrix of any dimension, aka any context size, at a time we are going to by no means materialize the complete consideration matrix, solely part of it at all times.
4. We managed to fuse collectively all of the ops right into a single kernel, lowering HBM entry significantly.

Closing SRAM utilization stands though at 4BD + 2B, the place B was initially calculated as M/4d the place M is the SRAM capability. Unsure if am lacking one thing right here. Please remark if you recognize why that is the case!

Block Sparse Consideration and V2 and V3

I’ll preserve this brief as these variations preserve the core concept however found out higher and higher methods to do the identical.

For Block Sparse Consideration,

1. Take into account we had masks for every block like within the case of causal consideration. If for a given block we’ve the masks all set to zero then we will merely skip all the block with out computing something actually. Saving FLOPs. That is the place the key positive aspects had been seen. To place this into perspective, within the case of BERT pre-training the algorithm will get a 15% enhance over one of the best performing coaching setup on the time, whereas for GPT-2 we get a 3x over huggingface coaching implementation and ~ 2x over a Megatron setup.

2. You possibly can actually get the identical efficiency in GPT2 in a fraction of the time, actually shaving off days from the coaching run, which is superior!

In V2:

1. Discover how at the moment we will solely do parallelization on the batch and head dimension. However in case you merely simply flip the order to take a look at all of the column blocks for a given row block then we get the next benefits:
   1. Every row block turns into embarrassingly parallel. How you recognize that is by trying on the illustrations above. You want all of the column blocks for a given row block to totally kind the eye output. When you had been to run all of the column blocks in parallel, you’ll find yourself with a race situation that may attempt to replace the identical rows of the output on the identical time. However not in case you do it the opposite approach round. Though there are atomic add operators in triton which might assist, they might doubtlessly set us again.
   2. We are able to keep away from hitting the HBM to get the worldwide Ms and Ls. We are able to initialize one on the chip for every kernel.
   3. Additionally we wouldn’t have to scale all of the output replace phrases with the brand new estimate of L. We are able to simply compute stuff with out dividing by L and on the finish of all of the column blocks, merely divide the output with the most recent estimate of L, saving some FLOPS once more!
2. A lot of the advance additionally comes within the type of the backward kernel. I’m omitting all of the backward kernels from this. However they’re a enjoyable train to attempt to implement, though they’re considerably extra advanced.

Listed here are some benchmarks:

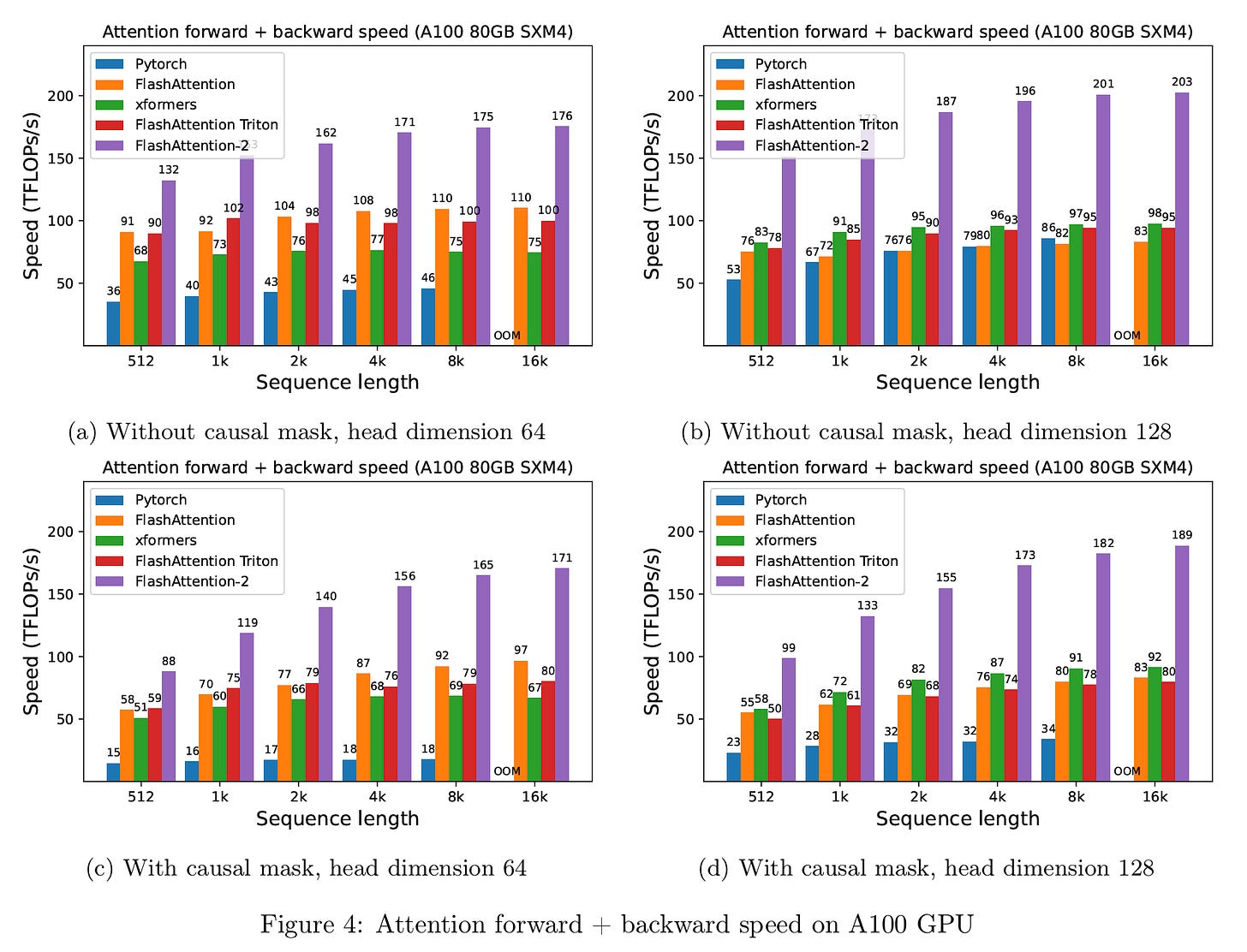
The precise implementations of those kernels must have in mind varied nuances that we encounter in the actual world. I’ve tried to maintain it easy. However do test them out right here.

Extra not too long ago in V3:

1. Newer GPUs, particularly the Hopper and Blackwell GPUs, have low precision modes (FP8 in Hopper and GP4 in Blackwell), which may double and quadruple the throughput for a similar energy and chip space and extra specialised GEMM (Normal Matrix Multiply) kernels, which the earlier model of the algorithm fails to capitalize on. It is because there are numerous operations that are non-GEMM, like softmax, which reduces the utilization of those specialised GPU kernels.
2. The FA v1 and v2 are primarily synchronous. Recall within the v2 description I discussed that we’re restricted when column blocks attempt to write to the identical output pointers, or when we’ve to go step-by-step utilizing the output from the earlier steps. Nicely these fashionable GPUs could make use particular directions to interrupt this synchrony.

3. Additionally they tailored the algorithm to focus on these specialised low precision Tensor cores on these new units, considerably rising the FLOPs.

Some extra benchmarks:

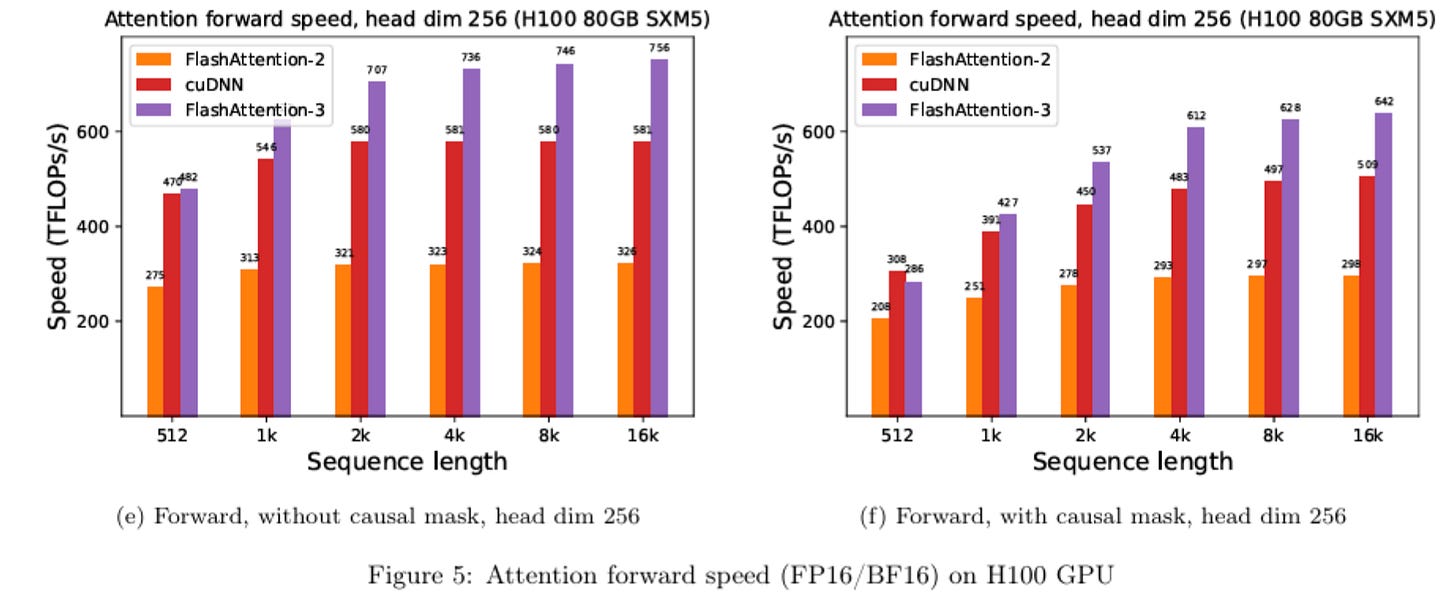
Conclusion

There’s a lot to admire of their work right here. The ground for this technical ability stage usually appeared excessive owing to the low stage particulars. However hopefully instruments like Triton might change the sport and get extra folks into this! The long run is shiny.

References

[1] Qwen 2.5-7B-Instruct-1M Huggingface Mannequin Web page

[2] Tri Dao, Daniel Y. Fu, Stefano Ermon, Atri Rudra, and Christopher Re, FlashAttention: Quick and Reminiscence-Environment friendly Precise Consideration with IO-Consciousness

[3] Tri Dao, FlashAttention-2: Quicker Consideration with Higher Parallelism and Work Partitioning

[4] NVIDIA Hopper Structure Web page

[5] Jay Shah, Ganesh Bikshandi, Ying Zhang, Vijay Thakkar, Pradeep Ramani, Tri Dao, FlashAttention-3: Quick and Correct Consideration with Asynchrony and Low-precision

[6] Single-precision floating-point format, Wikipedia